はじめに
エンジニアの齋藤です。基本情報技術者試験の勉強をしていて 科目AにもBにも二分探索木というものがでてきて詳しく知りたいと思ったのでまとめてみました。
二分探索木とはなにか
データ構造の1つでグラフの木構造を利用しています
…これだけではいまいち意味がわからないので1つ1つ単語ごとにまとめます
グラフ構造
データをノード(頂点)とエッジ(辺)の集合で表したデータ構造です。
ノードがいくつかあってノードのペアがエッジで結ばれています
グラフは実世界の様々なものを表現できます。
グラフを用いることでデータ間の複雑な関係性を視覚的に表現できて関係性を明確にできます。
逆に大規模なグラフは理解や操作が難しくなることがあります。
実際にSNSでのおすすめユーザーの提案やマップアプリでの最速ルートを求める機能などはグラフ構造と最適なアルゴリズムをつかうことによって実現されています
グラフイメージ
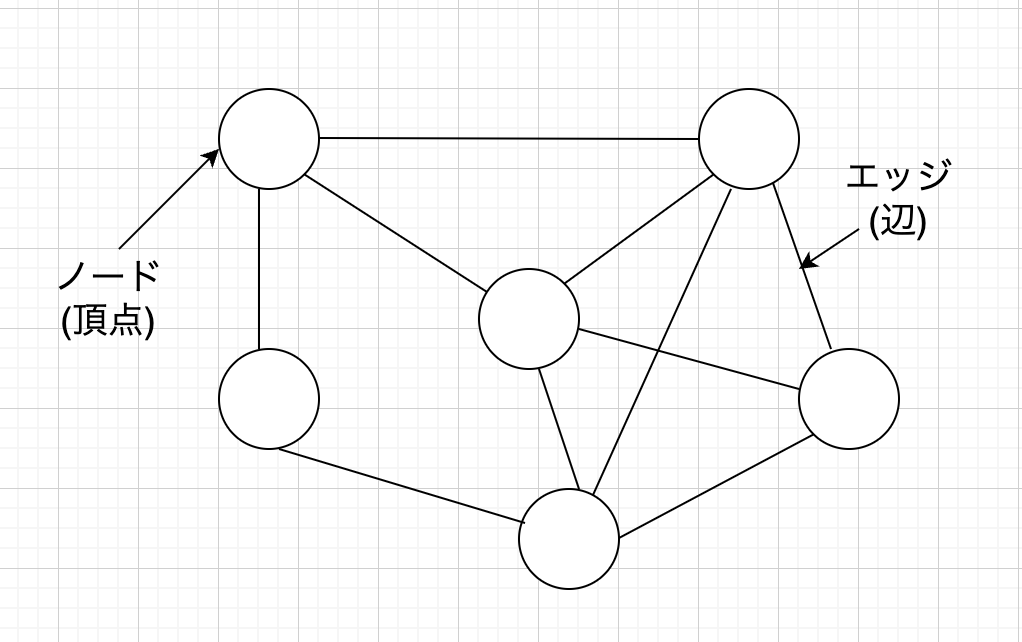
実際に実世界のものを表現するとしたら
- 交通 ノード→都市や駅、エッジ→道路や路線
- コンピューター ノード→端末、エッジ→ケーブル
- 社会関係 ノード→人間、エッジ→関係
木構造とは
ルート(根)を持つ階層的なデータ構造のことを指します。グラフの一種であり、サイクル(閉路)が存在しないことが特徴です。各階層は親子関係を持っており、親は複数の子を、子はただ一つの親を持ちます。
親子関係を明確に表現できるため、ファイルシステムなどの階層型データの管理に適しています。
投稿A ├─ コメント1 │ ├─ 返信1-1 │ ├─ 返信1-2 ├─ コメント2 ├─ 返信2-1
木構造イメージ
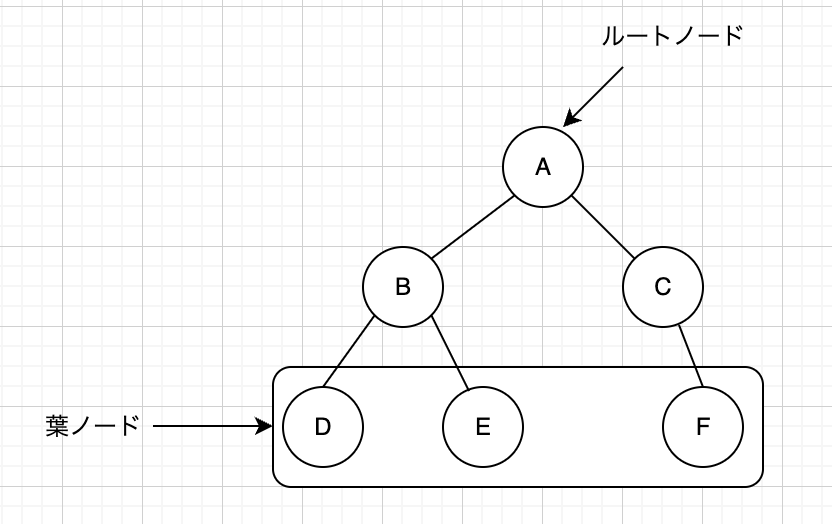
木構造の基本要素
- ルートノード (根)
- A がルートノード(木の最上位にあり、親を持たないノード)
- 親ノード & 子ノード(節)
- A は B, C の親ノード
- B は D, Eの親ノード
- C は Fの親ノード
- D, E, F はそれぞれの親を持つ子ノード
- 葉ノード
- D, E, F は子ノードを持たないため葉ノード
- エッジ(枝)
- A → B, A → C, B → D などのつながり
なお、どのノードをたどっても、同じ場所に戻るルートがないため、サイクル(閉路)は存在しない。
閉路:同じ点を2回以上通らずたどりはじめの点に戻るようにたどったもの
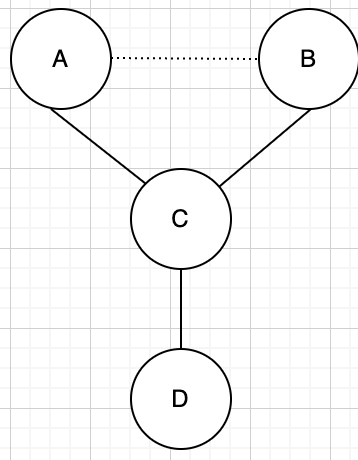
サイクルの例(閉路ありのグラフ)
サイクル(閉路): A → B → C → A
二分探索木とは
大量のデータから目的の値を探す場合、各階層の親ノードの値と比較して2つある分岐のうちのどちらの木を探索していくかを選択するたびに、探索対象を全体の半分に絞り込んでいくことができるので効率的です。
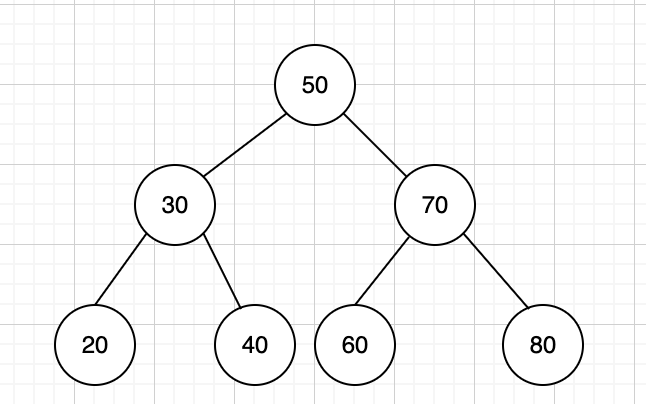
各ノードは最大2つの子ノードを持ち、左の子ノードの値 < 親ノードの値 < 右の子ノードの値になっています。
ですが、準備段階でデータがソートされていなければなりません。また、処理の途中でデータが変化する場合、適宜ソートしなおす必要もあります。
二分探索木
メリット
- データが常にソートされた状態で保持されるため、昇順または降順にデータを取得する操作が簡単に行えます。
「X 以上 Y 以下のデータを取得したい」などのクエリが多い場合
例えば上の図で30以上40以下のデータを取得するとしたら、根の50を見て40以下なので左のノードしか見なくていい
デメリット
- ランダムアクセスが必要なとき …etc
→インデックス指定の要素は取得できない
二分探索木をjavascriptで擬似的に作ってみる
<!DOCTYPE html> <html lang="ja"> <head> <meta charset="UTF-8"> <meta name="viewport" content="width=device-width, initial-scale=1.0"> <title>Binary Search Tree Example</title> </head> <body> <h1>Binary Search Tree Example</h1> <script> class Node { constructor(value) { this.value = value; // ノードの値 this.left = null; // 左子ノード this.right = null; // 右子ノード } } class BinarySearchTree { constructor() { this.root = null; // 木の根 } // ノードを挿入するメソッド insert(value) { const newNode = new Node(value); if (this.root === null) { this.root = newNode; // 木が空なら新しいノードを根に設定 } else { this.insertNode(this.root, newNode); // 根から探索して挿入 } } // ノードを適切な位置に挿入するためのメソッド insertNode(node, newNode) { if (newNode.value < node.value) { // 新しい値が小さい場合は左子ノードに挿入 if (node.left === null) { node.left = newNode; } else { this.insertNode(node.left, newNode); // 左部分木に再帰的に挿入 } } else { // 新しい値が大きい場合は右子ノードに挿入 if (node.right === null) { node.right = newNode; } else { this.insertNode(node.right, newNode); // 右部分木に再帰的に挿入 } } } } const bst = new BinarySearchTree(); bst.insert(50); bst.insert(30); bst.insert(70); bst.insert(20); bst.insert(40); bst.insert(60); bst.insert(80); console.log(bst); </script> </body> </html>
Node クラス
- 役割: 二分探索木の各ノードを表します。
- プロパティ:
value: ノードの値を保持します。left: 左の子ノードを指します。right: 右の子ノードを指します。
BinarySearchTree クラス
- 役割: 二分探索木全体を管理します。
- プロパティ:
root: 木の根ノードを指します。
- メソッド:
insert: 新しいノードを作成し、木が空ならそれを根にする。そうでなければinsertNodeを使って適切な位置に挿入する。insertNode****: 現在のノードと比較し、新しいノードを左または右の子として適切な位置に挿入する。再帰的に呼び出しながら木を辿る。
データ挿入の流れ
根ノード作成
bst.insert(50);
Node クラスのコンストラクタが呼び出され、value 50 を持つ新しいノードが作成されます。
この新しいノードの left と right プロパティは null です。
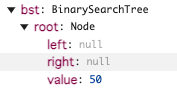
左子ノード作成(親ノード50)
bst.insert(30);
newNode のvalue 30が挿入される
this.root は先程のNode になるので this.insertNode(this.root, newNode); の処理へ
insert(value) {
const newNode = new Node(value);
if (this.root === null) {
this.root = newNode; // 木が空なら新しいノードを根に設定
} else {
this.insertNode(this.root, newNode); // 根から探索して挿入
}
}
node.valueは50でnewNode.valueは30なのでnode.left でthis.insert が実行されnode.leftがnull なので新しいノードがその位置に設定されます。
newNode は下記のようになる

insertNode(node, newNode) {
if (newNode.value < node.value) {
// 新しい値が小さい場合は左子ノードに挿入
if (node.left === null) {
node.left = newNode;
} else {
this.insertNode(node.left, newNode); // 左部分木に再帰的に挿入
}
} else {
// 新しい値が大きい場合は右子ノードに挿入
if (node.right === null) {
node.right = newNode;
} else {
this.insertNode(node.right, newNode); // 右部分木に再帰的に挿入
}
}
}
実行された後
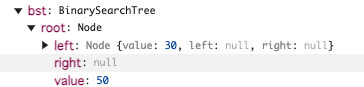
右子ノード作成(親ノード50)
bst.insert(70);
node.valueは50でnewNode.valueは70なのでif (newNode.value < node.value) の条件に入らずelse の処理に入る
if (node.right === null) {
node.right = newNode;
}
今度はnode.rightがnull なのでnode.right に新しいnode が挿入される
実行された後
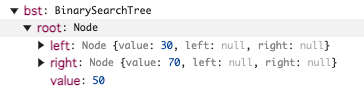
bst.insert(20); (親ノード30)
newNode.valueが20でnode.value が50になります。
if (newNode.value < node.value) { // 新しい値が小さい場合は左子ノードに挿入 if (node.left === null) { node.left = newNode; } else { this.insertNode(node.left, newNode); // 左部分木に再帰的に挿入 }
今度のnode.left は下記のとおり(valueが30)

nodeがnullではないので下記の処理に入る
this.insertNode(node.left, newNode); // 左部分木に再帰的に挿入
第一引数のnode.left は以下になる
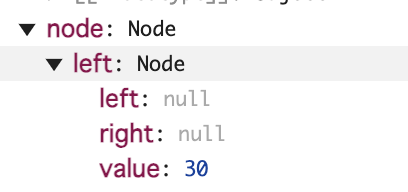
今度のnode.left はnullになり、新しいノード(value20)がその位置に設定されます。
if (node.left === null) {
node.left = newNode; // 新しいノードを作成
}
node.left に新しいノードが設定されます。
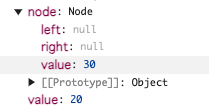
実行した結果
これで葉ノードである20が作成されます。
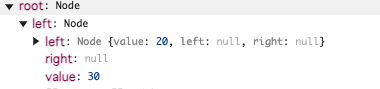
bst.insert(40); (親ノード30)
newNode.valueが40でnode.value が50になります。
また、if (node.left === null) でもないので以下の処理にはいる(node.leftのvalueは30)
this.insertNode(node.left, newNode); // 左部分木に再帰的に挿入
第一引数のnode.left は以下になる

newNode.value(40) < node.value(30)なので以下の処理になる
if (node.right === null) { node.right = newNode; }
node.rightはnullなのでnode.right に新しいnode value 40 が挿入される
実行した結果
これで葉ノードである40が作成されます。

右70の子ノードもこのように行っていく
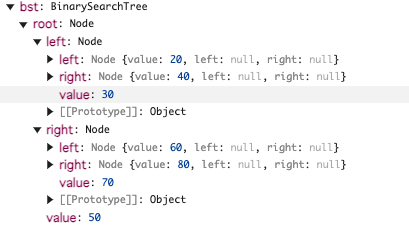
bst.insert(60); bst.insert(80);
下記のようになり二分探索木を表現できます
まとめ
二分探索木について理解があいまいだったので、これを機に詳しく調べられてよかったです。
取り扱いを間違えると最悪のパフォーマンスになってしまうことがあるようなので、機会があればそれについても調べたいです。
最後になりますが、現在弊社ではエンジニアを募集しています!
この記事を読んで少しでも興味を持ってくださった方は、ぜひカジュアル面談でお話ししましょう!
iimon採用サイト / Wantedly / Green