1.はじめに

こんにちは！株式会社iimonでフロントエンドエンジニアをしてる「みよちゃん」と申します！

チームメンバーの誰も「みよちゃん」と呼んでくれないので、そろそろ自称するのを辞めようかと悩んでいます。。

そんなことはさておき、今回のテーマは「コンピューターはどうやって計算しているのか」についてです。我々は業務の中で当然のようにコンピューターを使用していますが、コンピューター内部で行われている計算に関して考えることはそれほど多くありません。普段気にせずとも特別業務に支障は出ない内容ですが、うろ覚えだったため復習も兼ねて調べたため以下にまとめたいと思います。

2.論理演算

まず、コンピューター内部での計算を考える上で論理演算の理解が必要不可欠であるため、簡単に論理演算についておさらいしたいと思います！

論理演算とは

人間の思考を数学に取り入れたもの(らしいです。。)

その内容が「真」または「偽」のいずれかと判定できる文で、真は1として、偽は0として表します。

論理演算の種類

論理和(OR)
論理積(AND)
排他的論理和(ExclusiveOR, EOR, XOR)
否定(NOT)

NORやNANDなども論理演算に含まれますが、基本的にはこれら四つを組み合わせたものであるため、ここでは割愛させていただきます。

論理和(A OR B)

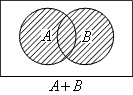
入力A・Bのいずれか一方でも1の場合に1を出力します。

入力A	入力B	出力
1	1	1
1	0	1
0	1	1
0	0	0

論理積(A AND B)

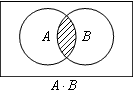
入力A・Bどちらも1の場合のみ1を出力します。

入力A	入力B	出力
1	1	1
1	0	0
0	1	0
0	0	0

排他的論理和(A XOR B)

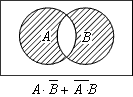
入力A・Bいずれか一方のみ1の場合に1を出力する

入力A	入力B	出力
1	1	0
1	0	1
0	1	1
0	0	0

否定(NOT A)

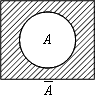
結果を反転し、1が入力された場合は0を、0が入力された場合は1を出力します。

入力A	出力
1	0
0	1

電子回路等で実現しやすい(トランジスタなど)ため、これらの演算が使用されています。

論理演算で実装した回路のことを論理回路と言います。

3.半加算器と全加算器

これらの演算子を組み合わせて作られた主要な演算回路を二つ紹介します。1 bit同士の加算をするものをを「HA(半加算器)」下位bitからの桁上がりを考慮して加算するものを「FA(全加算器)」と言います。

半加算器

HAは足し算の最下位bitの加算に使用されています。最下位bitの加算に必要な条件を考えてみましょう。

最下位bitの加算算に必要なのは

①次の位への繰り上がりの有無

②最下位bitの計算

これらを論理演算で表すと

①AND

②XOR

となります。HAはAND演算とXOR演算を組み合わせたものになります

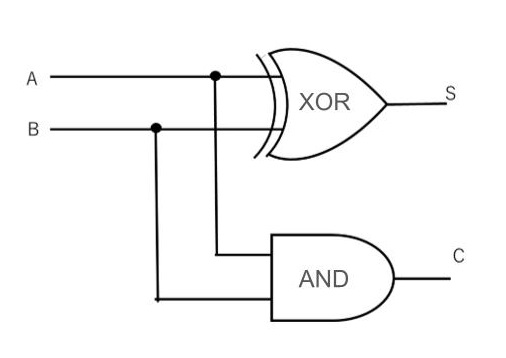
全加算器

FAは中間bitの計算に使用されます。FAは、HAの機能に加えて下位bitからの桁上がりを考慮する必要があります。

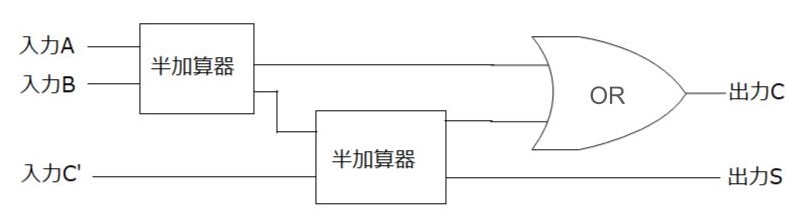
4.全加算器・半加算器使用した加算・減算

2進数の加算・減算はFAとHAを使用することで実現できます。

今回は加算回路と減算回路について解説したいと思います。

加算

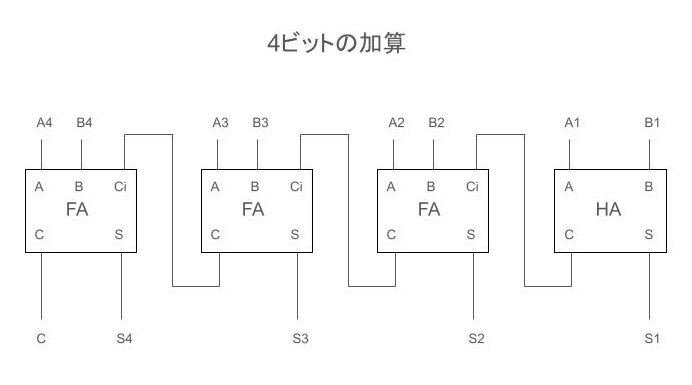
以下の例は４bitの２進数を加算するための加算回路です。

最下位bitは桁上がりを考慮する必要がないため、HAを使用し、それ以外は桁上がりを考慮するFAを組み合わせています。

それでは0110+0111を上の加算回路を使用して計算してみたいと思います

それでは数字を当てはめていきましょう

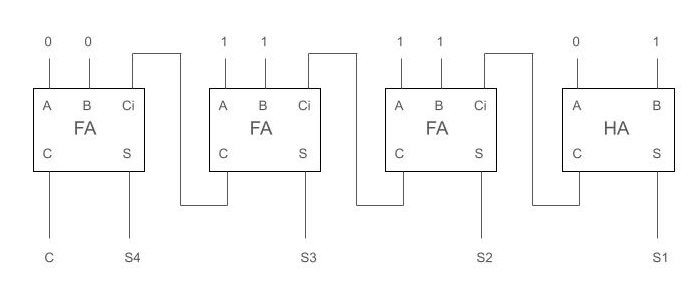
C⇒0, S4⇒1, S3⇒1, S2⇒0, S1⇒1

となりますので、解は1101ですね。

この計算は10進数で表すと6+7で和は13になります。これは二進数で表現すると1101であるため、加算回路を使用した計算は正しいことがわかります！

減算

補数を用いた減算の考え方

コンピューター内部では補数と呼ばれるものを使用し、減算を加算として扱っています。

補数とは、元の数字に足したときに桁上がりする最小の数のことです。

10進数で考えると4の補数は6、48の補数は52ということになります。

具体的には、(引かれる数) + (引く数の補数)の桁上がりを無視したものは減算と同じになります。

これだけではピンと来ないと思うので、実際に10進数で計算してみましょう。

50-30を例に挙げて考えてみます。

30の補数は70ですので、50(引かれる数) + 70(引く数の補数) = 120となります。ここから桁上がりを無視すると解は20となります。これは50-30の解と一致するかと思います。

今度は2進数で考えてみましょう。

1001の補数は0111、1100の補数は0100となりますね。

ここでお気づきの方もいらっしゃるかもしれませんが、2進数の補数とは対象の数字をbit反転したものに+1したものとなります。(詳細な説明は長くなるので省略します。)

つまり補数を用いた2進数の減算は

引く数をbit反転し、+1した上で引かれる数と加算し桁溢れを無視する

と表現することができます。

減算回路

この考え方を用いて4bit同士の減算回路を考えてみましょう。ここで先ほど説明した2の補数を使用した減算を使用して計算します。

減算回路では、1を足すためにHAを使用せず、FAのみを使用し、最下位bitの桁上がり部分に1を入力します。

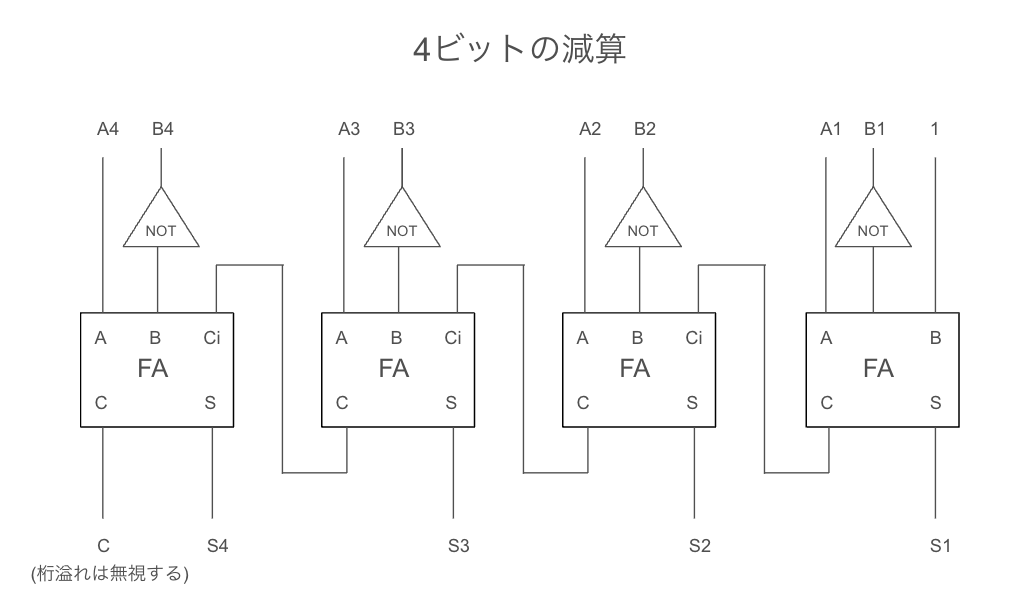
それでは実際に1100-0110を当てはめてみましょう。

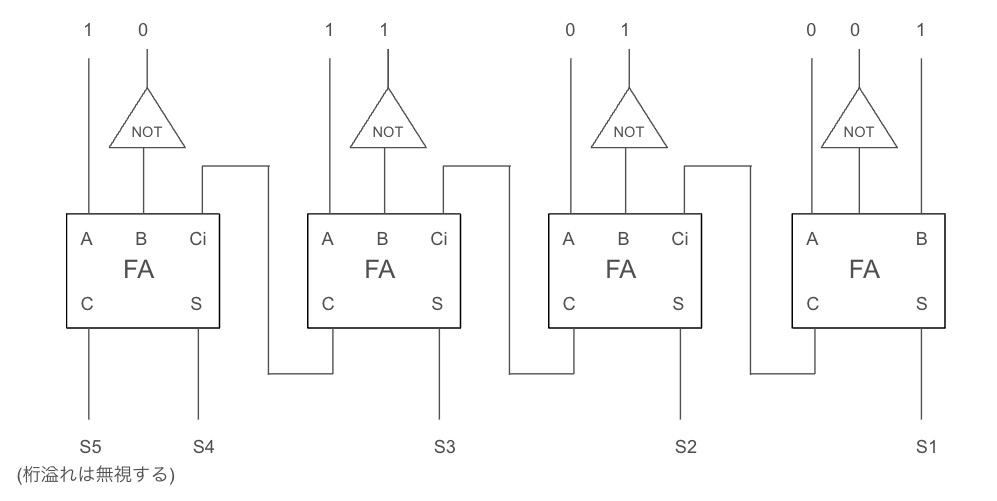
これを計算すると10110となります。先ほど説明した通り桁上がりは無視するため、解は0110となります。

10進数に変換して計算してみると12(1100) - 6(0110) = 6(0110)ですので、上記の回路を使用した計算は正しいことがわかります。

5.まとめ

今回は、論理演算とそれを利用した加算・減算の考え方についてまとめました。加算・減算回路以外にも、加減算回路や徐算回路・乗算回路などもありますが、自分自身しっかりと理解できていないので、今後はこれらに関しても理解を深めたいと思います。また、普段はあまり深く考えることがなくとも、コンピューター内部でどういったことが行われているか、エンジニアとしてもっと知っている必要があると思うので、より理解を深めなければならないと実感しました。

ここまで読んでいただきありがとうございました。今回の記事を読んで弊社に少しでも興味を持ってくださったあなた！！

弊社ではエンジニアを募集しております！

ぜひカジュアル面談でお話ししましょう！

ご興味ありましたら、以下のリンクからご応募ください！！ Wantedly / Green